摘要：本文阐述了根据线性代数定理，通过计算机代码实现自动编制设备点位表的过程，并给出实例和成果。

关键词：矩阵、向量、Python、设备点位表

一、前言

线性代数在数学、物理学和技术学科中有各种重要应用，因而它在各种代数分支中占居首要地位。随着科学的发展，我们不仅要研究单个变量之间的关系，还要进一步研究多个变量之间的关系，各种实际问题在大多数情况下可以线性化，而由于计算机的发展，线性化了的问题又可以被计算出来，线性代数正是解决这些问题的有力工具。

在设计弱电系统中，设备点位表是必不可少的设计文件组成部分。根据中华人民共和国住房和城乡建设部颁布的《建筑工程设计文件编制深度规定》中“5.3 建筑智能化设计”，规定在初步设计文件阶段，必须需要提供系统图。在安全技术防范项目设计中，设计人员需要编制前端设备点位表。常规做法是设计人员在EXCEL软件中手工编制前端设备点位表。当系统较大或前端设备较多时，设计人员的工作量较大，且容易出错。

笔者通过实践，在安全技术防范系统中，特别是以住宅小区为代表，其入侵和紧急报警系统、对讲系统以及电子巡查系统中的点位相对较多，也有一定的规律，可以采用线性代数中矩阵、向量等概念予以定义，借助计算机进行线性代数的函数运算，通过计算机辅助计算与设计，直接、快速、准确、高效地生成前端设备点位表。

本文通过某一个住宅小区的具体案例，建立结构化数学模型，编制计算机程序语言，生成前端设备点位表的过程，予以阐述。

二、用Python生成前端设备配置表

(一)线性代数基本概念

由于线性代数在数学、物理学、计算机科学中均有定义，有些一致，有些不一致，为防止概念混淆，本文中提到的术语、概念先以数学中的定义为准，当计算机科学中另有定义时，以为计算机科学中为准。

1、矩阵

矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合(注：这里借用数学上对矩阵的定义)。如本文表1的前4列可以独立形成一个矩阵，可以表示在这个住宅小区建筑的基础数据。

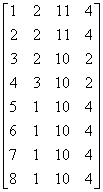
将这个矩阵记作Λ

2、向量

在数学中，向量(也称为欧几里得向量、几何向量、矢量)，指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向;线段长度：代表向量的大小。与向量对应的量叫做数量(物理学中称标量)，数量(或标量)只有大小，没有方向。

几何向量的概念在线性代数中经由抽象化，得到更一般的向量概念。本文中提到的向量，定义为向量空间的元素。这个定义更加接近计算机科学中的定义。

如本文表2，把红外探测器用D来代表，紧急按钮用A来代表，按照设备的顺序，

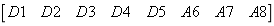
这个向量记作：Κ

3、函数

在数学中，函数的定义为：如果当变量x在其取值范围内任意取定一个数值时，量y 按照一定的法则总有确定的数值和它对应，就称y是x的函数，记作y=f(x),x叫自变量，y也叫因变量。

线性代数中一个矩阵与向量运算，输出到向量示意如下：

函数(图1)

需要的结果就记作：

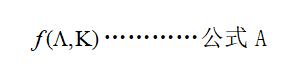
(二)原始数据的描述

假设一个住宅小区有8栋楼，1#2#楼各有2个单元，楼高11层，每层4户，含A1,A2房型;3#楼有2个单元，楼高10层，每层2户，含C1房型;4#楼除了有3个单元外，其他与3#楼一致;5#楼有1个单元，楼高10层，每层4户，含A1,A2房型;6#楼有1个单元，楼高10层，每层4户，含B1,A2,B2房型;7#楼有1个单元，楼高10层，每层4户，含A1,A2房型;8#楼有1个单元，楼高10层，每层4户，含B1,A2,B2房型。

经过平面图初步设计后，确定A1房型需设置5个红外探测器，3个紧急按钮;A2房型需设置4个红外探测器，2个紧急按钮;B1和B2房型均需设置7个红外探测器，4个紧急按钮;C1房型需设置8个红外探测器，4个紧急按钮。每种房型均设置1台报警控制键盘。其他房型依次类推。

经过整理后如下表(1-3)：

楼栋情况汇总表(表1)

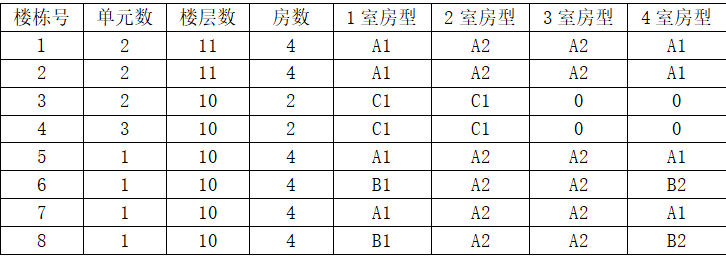
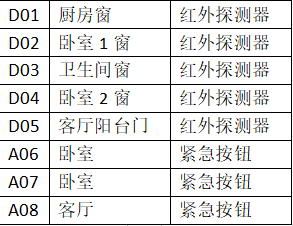
A1房型前端设备设置表(表2)

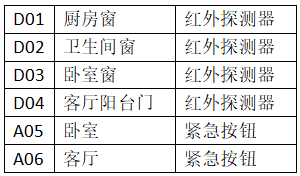
A2房型前端设备设置表(表3)

其他房型略

(三)针对以上原始数据的分析

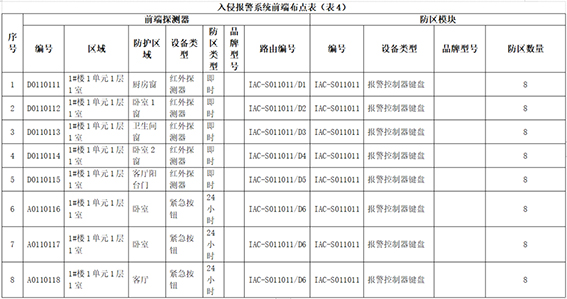
在实际的项目设计中，需要得到的前端设备点位表的格式如下：

经过对以上表4的分析，将“1#楼1单元1层1室”这个地点指定一个代码，这个代码可由表1通过矩阵生成，定义为“0111011”这个字符串，这个字符串代表1#楼1单元1层1室这套房。

以上表1中的房号、房型分别对应表2表3。1#楼1单元1层1室这套房里需要安装的设备，我们可以从表2中找到。那么防区模块的编号就可以定义为IAC-S011011，这套住宅里的第1个红外入侵探测器的唯一编号就定义为D0110111，路由编号的意思是该红外探测器位于防区模块的第1个防区，定义为：IAC-S11011/D1。其他前端设备以此类推。

上段文字中的这几个代码0111011、IAC-S011011、D0110111、IAC-S11011/D1从计算机科学来说均不是数值而是字符串，这些字符串是由包含数字的矩阵和向量通过函数运算而生成的。

用表1的前四列数据构建出下面矩阵Λ₁，这个矩阵代表小区到房的基本数值。

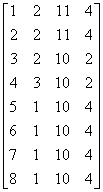
Λ₁

表1的后四列数据构建出矩阵Λ₂代表房型。

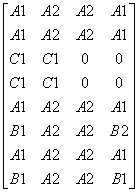
Λ₂(0表示没有)

把表2、3分别构建矩阵K₁-K₂代表不同房型内前端设备的安装情况。

A1房型：

K₁

A2房型：

K₂

D代表红外探测器，A代表紧急按钮，后面的数值代表安装位置序号，并由此计算出防区。

由这个矩阵

的来源，红框位置的值代表了一个楼面有多少间房间，同时也是一个隐含向量的最后一个值，这个隐含向量是正整数从1至红框内值的数列。如第1行的向量就可以如下表示：[1 2 3 4]，第3行的向量就是：[1 2]，经过矩阵与向量的计算机函数运算，可以得到1号楼1单元1层1室的室号“0111011”这个字符串，这个室号就是表7中模块编号的核心部分。这个隐含向量还有个作用，就是与矩阵Λ₂形成映射关系，从物理位置上指向某一个房型，也可以说再次映射到矩阵K₁-K₂.这个映射关系，如下图显示了1号楼1单元1层1室映射关系，其他房以此类推可以构建出整个小区家防报警前端设备设置的结构化数学模型，得到输出的表7。根据刚才推导出的公式A，下一步就是编制代码，实现以上功能。

各个矩阵与向量关系图(图2)

(四)计算机代码的实现

1、代码语言的选择

Python 是由 Guido van Rossum 在八十年代末和九十年代初，在荷兰国家数学和计算机科学研究所设计出来的。是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。设计具有很强的可读性。选择Python作为此次代码编写工作的原因是Python具有丰富的库、可在UNIX，Windows和Macintosh兼容等特点。在Python有若干向量运算的库，也可用Python内置的“列表”数据来生成矩阵与向量。本文中的代码采用“列表”方式生成矩阵和向量，通过运算编制EXCEL格式的电子表格文件。

2、代码流程图

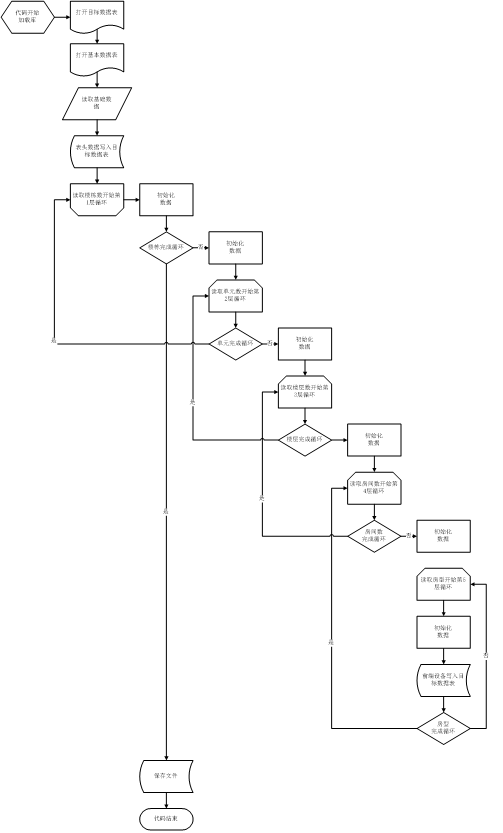
前端点位表代码流程图(图3)

3、代码生成

根据代码流程图编制代码。由于代码较长，限于篇幅本文从略。

4、其他说明

代码的编制环境：PY3.8，引用的库有：xlwing,os,time,math等。

四、结束语

本文阐述了根据线性代数的部分定理，通过计算机代码直接生成智能化工程的前端点位表，为智能化设计探索了新的途径。在编制前端点位表时，找出其规律性，编制代码由计算机生成需要的文件，从而减轻工作量，提供准确率。

参考文献

1、《建筑工程设计文件编制深度规定》 住房和城乡建设部 2016年11月批准

2、《数学指南-使用数学手册》 埃伯哈德.蔡德勒 科学出版社 2012年1月

3、《疯狂Python讲义》 李刚 电子工业出版社 2019年1月

4、《Python办公自动化》 龙豪杰 中国水利水电出版社 2021年3月